Área do losango

O losango é um quadrilátero (polígono com quatro lados) que possui lados opostos paralelos e congruentes (todos os lados tem a mesma medida) e duas diagonais que se interceptam exatamente no ponto médio de cada uma e são perpendiculares. Todo losango é também paralelogramo.


Como as diagonais do losango se interceptam em seus pontos médios sob um ângulo reto (formam um ângulo de 90°), podemos obter a área do losango a partir da área de um retângulo.
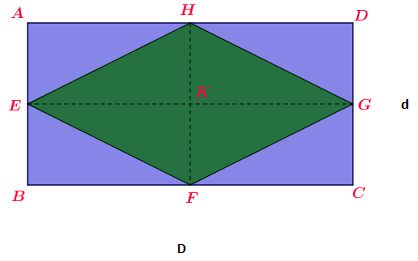
Considere o losango cujas medidas das diagonais são D (diagonal maior) e d (diagonal menor):

Pelos vértices do losango, traçamos paralelas às diagonais e obtemos o retângulo ACBD:

O losango ocupa a metade da superfície do retângulo ABCD. Como a área do retângulo é:
A = b . h
Então a área do losango é:

Onde b = d e h = D
b é a medida da base do retângulo
d é a medida da diagonal menor do losango
h é a medida da altura do retângulo
D é a medida da diagonal maior do losango
Temos então:

Podemos também obter a área do losango de outra maneira:

Onde:

• l é a medida dos lados do losango
• d é a medida da diagonal menor, pois é a menor diagonal
• D é a medida da diagonal maior

Se olharmos para a figura abaixo, o losango nada mais é que a união de dois triângulos congruentes, ou seja, triângulos iguais com todas as medidas iguais.

Então basta somarmos as áreas dos dois triângulos e vamos obter a área do losango. Portanto vamos fazer isso, somar a área dos dois triângulos. Como os dois triângulos têm a mesma medida, basta pegar o dobro da área.
Sabemos que a área do triângulo é 

Porém b = d e h = D / 2 . Onde:

• b é a medida da base do retângulo
• d é a medida da diagonal menor do losango
• h é a medida da altura do retângulo
• D/2 é a medida da metade da diagonal maior do losango

Então o dobro da área do triângulo é:

Multiplicamos por dois porque queremos o dobro.
Temos que:

ou seja, a área do losango é diagonal menor multiplicado pela diagonal maior dividido tudo por dois.